(..Table Part..)	Contents	Index	(..Table Part)

4.2.3 Local Rule Table (Table)

Each table is started with the keyword

(The end of a table is either the begin of an additional table or at the same time the end of the entire SDL program.) After TABLE we place the already discussed entries of the form

One table may contain as many entries as we want.
 
Remark:
For both ConditionPart and Consequence end with a colon, it may be of advantage to think of a layout which makes it possible to oversee the structure. Because of the author's lack of imagination we simply suggest to set every second colon on tab.

For so far the syntax. In order to understand how such a table is interpreted by SCARLET, we remind once again of the properties, the local rule of a CA has got. It is a function that is in every time step simultaneously applied to each cell of the retina, in order to change their states depending on the states of certain cells in their neighbourhood. With we talk about a function from S^d to S, if S denotes the state set and the neighbourhood is of order d.
 

Now we are going to compare this to the structure of a local rule table as a whole (which should finally represent in SCARLET). For the features of the condition part as well as the consequence part have a big influence on it, they will be shown explicitely again there. Let us suppose that Entry₁, ... , Entry_m, are the entries of the table, c_i,1; c_i,2; ... ; c_i,ji , , all variable assignments of ConditionPart_i in right the order in which they are given there, except those which are ignored because of the nonstrict treatment. Let b_i, , be the boolean value of ConditionPart_i, then a SDL program with this table roughly implies the algorithm beneath:

c1,1; c1,2; ... ; c1,j1;

IF b1 == TRUE

   THEN Consequence1

   ELSE {c2,1; c2,2; ... ; c2,j2;

         IF b2 == TRUE

            THEN Consequence2

            ELSE {c3,1; c3,2; ... ; c3,j3;

      ...
           }
         } 

It describes what happens, when the table is applied to an arbitrary cell z. According to this, a single step of the simulation will certainly require as many calls of the table part as there are cells in the lattice. This is automatically done by SCARLET.
 

Remember furthermore that

• all variables are initialized before each call of the table,

• symbolic constants are only initialized before each simulation step, and

• the cells of the retina are updated only after each simulation step.

But back to the algorithm above. It says,

However, during one run of the table part, there will at most one consequence part of every table be executed. (We will soon see that a SDL program can consist of more than one table.) It is exactly the first one for which all conditions in ConditionPart are satisfied. This is remarkable, for the belonging Consequence is the only part which may affect the state of the site, or, to put it in other words, in which there can be assigned a value according to the function . In the next paragraph we will see which influence the order of the entries within a table has on the choice of that ConsequencePart that will be the affecting one.

Example 49:

We give again a look at example 46 in order to show the table in an algorithmic form:

IF center.state > 0; == TRUE
  THEN
    state++;
    state %= 3;
  ELSE 
    IF center.state==0; == TRUE
      THEN 
        sum = left.state&1 + ... ;
        IF (center.state==0; && sum <=3) == TRUE
          THEN SELF = {1};  

Note: sum is only calculated, if center.state == 0. That is the reason for the additional condition before sum = ... .

Order of the Entries

In order to show that the order of the entries in a table play quite an important part in the course of the simulation, we give the following example:

Example 50:

SIGMA signal; DIMENSION 1; REGISTER INT state; NEIGHBOUR left : (-1); TABLE left.state == 1; : SELF = {1}; : TRUE; : SELF = {0}; :

applied to the following 1-dimensional lattice with length l

causes a signal 1 to run from the left to the right side at "speed 1". Arriving there it disappears.

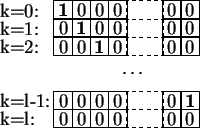
But just exchanging the two entries, the behaviour will be completely different: The signal disappears already after the first step.
The reason for that is obvious, because all the combinations of neighbour configurations for which condition 1 is satisfied form a subset of the ones which conform to condition 2.
If condition 2 had been given in a form which had left the intersection empty (left.state != 1;), an exchange would not have led to a different behaviour.

Source Code:	signal.sdl
	signal.rdl

Thus for not losing the track creating complexer tables, it seems indeed to be of advantage to follow the strategy we have put together:

Suppose that , are the entries of a table, the coordinate of the looked at cell, the n-dimensional neighbourhood of order d. In this paragraph, Mi will represent the set of all d-tuples for which the condition of entry Ei is satisfied, if for a configuration . We get the following rules: If , then the order in which Ei and Ej appear in the table does not matter. If , then entry Ei (with the more special condition) must precede Ej. All the other cases can be reduced to 1. or 2. by splitting up the sets Mi in a suitable way.

Nondirect State Assignments

We have to pay particular attention to the behaviour of a local rule table, if the generic cell does not receive its new state from a SelfAssignment unit. Such a situation rises, if

1. none of the entry conditions is fulfilled by the configuration of the neighbours.

2. The configuration of the neighbours fulfils a ConditionPart, but in the belonging Consequence

   1. does exist no SelfAssignment unit,

   2. the state of SELF is only changed in parts. (That means, only single registers are affected. )

In case of 1. and 2.1. the site keeps its old state. In case of 2.2. only the values of registers which have not been captured by the assignment stay unchanged.
But in every case the new state of a site depends on its old state in the previous time step!
 

That is no problem, if the site itself is a neighbour (that means, if belongs to the neighbourhood), for then dependencies of this kind are allowed. The table constructed in SDL still competes with the demands on the local rules in the abstract model.

But troubles arise, if the site to be changed should not be a neighbour! In this case the user has to take care by himself that situations as described above do not become reality, if he wants the table to represent a valid local rule.

While it is rather easy to avoid 2. (since it is sufficient to check each entry separately), for 1. it is sometimes so difficult that the only chance is to simply guarantee that the table is complete ( ; the definition of M_i can be found above.)

If the table should indeed stay incomplete, it must be granted that all neighbour configurations missing are really not assumed.

Remark:
Therefore, the appearance of the initial configuration must also be taken in account!

(..Table Part..)	Contents	Index	(..Table Part)