(..Statement Part..)	Contents	Index	(..Statement Part..)

3.2.3 Cell Grids (Loop)

Generally we are now able to specify the whole initial configuration by assigning CellExpressions to each cell, one by one. It need not be underlined, how boring this could be! Usually there are quite big amounts of cells which are to be treated in the same way. SCARLET supports this by giving a possibility to look at all cells in subsets of rather simple forms at the same time. The complete syntax is given by

The basic form of all these sets is the cube, which is completely determined by two diametral corners Cell. We have already used this method to fix the range of the retina itself. The cube must certainly be a part of the retina. (Therefore, it is sufficient to check that the coordinates of the corners are within the range of the retina.)

Besides the ''full cube'' we can also decide to consider only those sites which form the crossing points of special grids (grid points), in which the distances between two grid lines in a certain coordinate direction must be constant.
 

As most general syntax of a set of grid points Loop we have

where Cell₁ and Cell₂ are suitable sites generating the cube and lying within the retina, and where the single IntExpressions of (IntExpressionList) are values for the step sizes in the single coordinate directions. (IntExpression₁ belongs to the first, IntExpression₂ to the second, and so on.) Looking at a n-dimensional space we have to put n values for n step sizes.

Furthermore we restrict the step sizes to positive nonnegative numbers, and IntExpression_i, , can only be zero, if the cube's extension in coordinate direction i equals one, what means that the i-th components of Cell₁ and Cell₂ are the same.

Although the syntax of Loop looks like a DO-WHILE structure, SCARLET evaluates all its expressions - especially (IntExpressionList) - only once to grant the step size to be constant.

Note that SCARLET takes Cell₁ always for a grid point. Suppose that the set of coordinates of the full cube is called Q. The coordinate of a certain cell is a grid point, if there exist such that the following statement is valid:

Example 38:

In a two-dimensional space [-5,-3] (3,2) [5,4] generates the following set of grid points (pointed out by black dots):

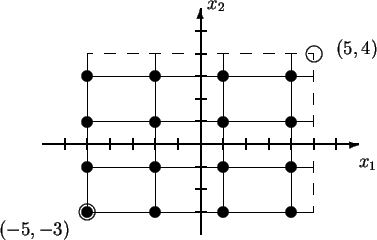
For some special cases SCARLET allows abbreviations instead of the normal syntax:
 

• If IntExpression is the common step size for all coordinate directions, it is sufficient to indicate it once like this
  Cell₁ (IntExpression) Cell₂
  
   

• If furthermore in this case IntExpression is equal to one - the whole cube is meant - then we may omit the parentheses and type
  Cell₁ .. Cell₂

Example 39:

Three ways to describe the same set:

[0,1,2,3] (1,1,1,1) [4,5,6,7]

[0,1,2,3] (1) [4,5,6,7]

[0,1,2,3]..[4,5,6,7] 

(..Statement Part..)	Contents	Index	(..Statement Part..)