SCARLET - Example 1 ("Life")


(CA in SCARLET..)	Contents	Index	(..CA in SCARLET)

1.2.2 Examples of Programs

In conclusion of the first chapter we would like to give the reader a first impression of SCARLET'S features. Therefore, the reader is certainly not expected to understand every detail of the programs shown in this paragraph. It seems to be more important to get a general idea of their structure, a main connecting thread, which may guide through the manual.

Example 1 ("Life")

Let us start with a famous example which helped a lot to make the theory of CA almost popular: The "Game of Life" invented by J. H. Conway in 1970. It was his intention to investigate the evolution of an idealized population of living beings. It does not matter much that we cannot implement "Life" in a two-dimensional cellular space, as it was suggested by Conway; we will take a retina that is finite, though big enough instead. Furthermore we use two states 0 and 1: A cell will represent a living organism, if its state is 1, and a dead one, if the state is 0. The neighbourhood will include the cell z refered to (generic cell) itself, together with the eight surrounding cells.

Fig. 3: Neighbourhood used for "Life".

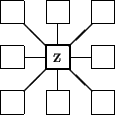
The evolution of the population obeys the following rules:

if exactly three cells in the neighbourhood are "alive", then the generic cell will become "alive" (state 1), too.
If exactly four neighbours are "alive", the generic cell will keep its old state.
In all other cases the generic cell will be "dead" (state 0).

Though these are very simple rules to model phenomenoms like the deadly consequences of a too high or too low population density, or the birth of new life under good conditions, the behaviour of such a system is already so complex that it could hardly be overseen. One reason for that surely is that the chosen rules are very balanced.


SIGMA life;

DIMENSION 2;

REGISTER INT state;

NEIGHBOUR  center       : ( 0, 0);
           left         : (-1, 0);
           right        : ( 1, 0);
           upper        : ( 0, 1);
           lower        : ( 0,-1);
           left_upper   : (-1, 1);
           right_upper  : ( 1, 1);
           left_lower   : (-1,-1);
           right_lower  : ( 1,-1);

VAR INT sum;

BORDER {0};


TABLE

   sum = center.state
	  + left.state + right.state + upper.state + lower.state 
	  + left_upper.state + right_upper.state
	  + left_lower.state + right_lower.state;

   sum==3; : SELF={1}; :

   sum==4; : /* no statement */ :

   /* TRUE */ : SELF={0}; :

The program given here can be recognized as a SDL program by the keyword SIGMA in the headline. It desribes what the local rule function will do to a single but arbitrary cell of the retina during one step of the simulation. The program consists of two parts: The first part reachs until TABLE and includes several declarations:

The space dimension is set on 2.
In SCARLET the state set is subdivided into smaller units, the registers. We distinguish between two types which have nearly the same ranges as string and signed integer variables in the programming language C. To model the states 0 and 1, we use an integer register and label it state.
Like in the abstract model, neighbours are indicated by relative positions and can be accessed by symbolic names, which are chosen by the user.
An integer variable sum is defined,
and finally the device BORDER {0}; will cause all cells on the boundary to remain in state 0 during the whole simulation (what seems to be a proper assumption to our model). Besides, boundary cells could in principle be treated like cells in the interior.

The second part shows the rules of evolution as kind of some (here: three) nested IF-THEN-ELSE statements (entries). Notice that all IF, THEN and ELSE parts are separated from each other by colons : . Everywhere in the table part, assignments to variables are allowed; Here, the total number of neighbours with state 1 is stored first in sum. Later sum is used to choose a proper action.
Observe that a non existent condition - like in entry three - equals TRUE and that the generic cell is left invariant, if there is no statement in the consequence part - like in entry two.


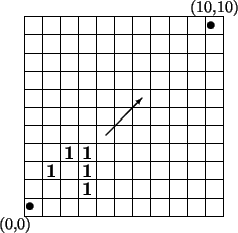
RETINA glider;

RANGE [0,0]..[10,10];

REGISTER INT state;

START
      [1,2]= {1};
      [2,3].state = 1;
      [3,1]..[3,3] = {1};

The RDL program shown above describes an initial configuration that matches the SDL program Life. Again we find a subdivision into a declaration and a statement part:

The chosen retina, which must always be a cube in SCARLET, is located in and has got the corners (0,0), (0,10), (10,0), and (10,10). (Just two diametral ones must be indicated.)
Corresponding to SIGMA Life there must appear an integer register in this program as well, which has got the same name state by coincidence.
The keyword START signals the beginning of the statement part, where 1 is assigned to several cells accessed by their position. As shown here it is possible to assign the whole state surrounded by {} (first and third line) as well as to store values to single registers (second line). The construction in the third line causes all cells within the rectangle, with corners given there, to be treated together.
The remaining cells are already in the desired state 0 because of the initialization of the retina, which is automatically done by SCARLET.

Applying the local rule Life to this initial configuration, the figure consisting of state-1-cells will appear again after five time steps, but shifted up and to the right one cell each.

By the way, the following strange-looking initial configuration answered the question raised by Conway, if there exist populations whose size will approach infinity in time, assuming that there is enough space. (Hint: The solution is close connected with the first figure.)


RETINA strange;

RANGE [-10,-10]..[30,40];

REGISTER INT state;

START
      [6,1]..[7,2]       = {1};

      [6,12]..[8,12]     = {1};
      [5,13] (4) [9,13]  = {1};
      [4,14] (6) [10,14] = {1};
      [5,15] (4) [9,15]  = {1};
      [6,16]..[8,17]     = {1};

      [4,22]..[6,22]     = {1};
      [3,23]..[7,25]     = {1};
      [5,23]..[5,24]     = {0};
      [2,26] (6) [8,26]  = {1};
      [3,26] (4) [7,26]  = {1};

      [6,31]..[7,31]     = {1};

      [4,35]..[5,36]     = {1};

Remark:
The device [5,15] (4) [9,15] = {1}; assigns 1 to a couple of cells within the rectangle [5,15] .. [9,15]: exactly to every fourth cells in each coordinate direction starting with the cell in [5,15].

Source Code:	life.sdl
	glider.rdl
	cannon.rdl


(CA in SCARLET..)	Contents	Index	(..CA in SCARLET)